本篇是《Rust与AI》系列的第二篇，上一篇我们主要介绍了本系列的概览和方向，定下了一个基调。本篇我们将介绍LLM的基本架构，我们会以迄今为止使用最广泛的开源模型LLaMA为例展开介绍。

LLM背景

Rust 本身是不挑 AI 模型的，但是 LLM 是当下最热的方向，我们就从它开始吧，先了解一些非常基础的背景知识。

Token

LLM 中非常重要的一个概念是 Token，我们输入给 LLM 和它输出的都是 Token。Token 在这里可以看做语言的基本单位，中文一般是词或字（其实字也是词）。比如：”我们喜欢 Rust 语言“，Token 化后会变成类似 ”我们/喜欢/Rust/语言“ 这样的四个词，可以理解为四个 Token。

给定一段任意的自然语言文本，我们可以用一个分词器（Tokenizer）将其 Token 化成一个个连续的 Token。这些 Token 接下来就可以映射成一个个数字，其实是在词表中的索引，索引进而可以找到一个稠密向量，用来表示该位置 Token 的语义输入。

我们以刚刚的”我们喜欢 Rust 语言“为例，假定已有词表如下。

……
1000 Rust
……
2000 我们
2001 喜欢
2002 语言
……

注意，前面的数字是行号，并不是词表内容。刚刚那句话其实就是 [2000, 2001, 1000, 2002]，这就是 LLM 的输入。LLM 拿到这些 ID 后，会在一个非常大的表里查找对应的稠密向量。这个非常大的表就是词表，大小是：词表大小N × 模型维度，如下所示。

……
1000 0.9146, 0.066, 0.4469, 0.3867, 0.3221, 0.6566, 0.2895, ...
……
2000 0.5702, 0.9579, 0.0992, 0.9667, 0.5013, 0.4752, 0.1397, ...
2001 0.2896, 0.7756, 0.6392, 0.4034, 0.3267, 0.9643, 0.4311, ...
2002 0.4344, 0.6662, 0.3205, 0.3929, 0.6418, 0.6707, 0.2414, ...
……

也就是说，输入”我们喜欢Rust语言“这句话，我们实际传递给模型的其实是一个 4×Dim 的矩阵，这里的 4 一般也叫 Sequence Length。

我们可以暂时把模型看作一个函数 f(x)，输入一个 Sequence Length × Dim 的矩阵，经过模型 f(x) 各种运算后会输出 Sequence Length × Vocabulary Size 大小的一个概率分布。有了概率分布就可以采样一个 Token ID（基于上下文最后一个 Token ID 的分布），这个 ID 也就是给定当前上下文（”我们喜欢Rust语言“）时生成的下一个 Token。接下来就是把这个 ID 拼在刚刚的 4 个 ID 后面（输入变成 5 个 ID），继续重复这个过程。

生成

如上所言，生成过程就是从刚刚的概率分布中 “选择” 出一个 Token ID 作为下一个 Token ID。选择的方法可以很简单，比如直接选择概率最大的，此时就是 Greedy Search，或 Greedy Decoding。

不过我们平时用到大模型时一般都用的是采样的方法，也就是基于概率分布进行采样。抛硬币也是一种采样，按概率分布（0.5，0.5）进行采样，但假设正面比较重，概率分布就可能变成了（0.8，0.2）了。基于 Vocabulary Size 个概率值进行采样也是类似的，只不过括号里的值就是词表大小那么多个。

top_p/top_k 采样是概率值太多了，大部分都是概率很小的 Token，为了避免可能采样到那些概率很低的 Token（此时生成的结果可能很不连贯），干脆就只从前面的 Token 里挑。

top_k 就是把 Token 按概率从大到小排序，然后从前 k 个里面选择（采用）下一个 Token；top_p 也是把 Token 按概率从大到小排序，不过是从累积概率大于 p 的 Token 里选。就是这么简单。

这里有个小细节需要说明，因为选择了 top_p/k，所以这些备选的 Token 需要重新计算概率，让它们的概率和为 1（100%）。

开源代表——LLaMA

接下来，我们把重心放在函数 f(x) 上，以最流行的开源 LLM——LLaMA 为例，简单介绍一下模型的结构和参数。

结构

LLaMA 的结构相对而言比较简单，如果我们忽略其中的很多细节，只考虑推理过程，看起来如下图所示。

图中 [] 中的是该位置的张量 shape，B 表示 Batch Size，一般时候都是批量丢给 GPU 计算的，L 就是 Sequence Length，D 就是上面提到的 Dim。这是一个简化了的架构图，但是足以清晰地表达模型了。

两个 Hidden states（以下简称 HS），外面（之上和之下）的部分我们前面已经提到过了（注意上面部分，[B,L,D] 会先变成 [B,L,VS]，然后取最后一个 Token 就得到了 [B,1,VS]），上面的 HS 会传回到 Block 里面，重复 N 次，N 就是模型的层数。接下来我们就把重点放在中间这个 Block 里。

每个 Block 包括两个主要模块，一个 MHA（Multi-Head Attention）模块，一个 FFN（Feedforward Network）模块，每次传给模块之前都需要 Normalization，这个叫 Pre-Normalization，一般用来稳定训练。另外，每个模块结束后会叠加模块之前的输入，这个叫残差连接，一般能加速收敛。

接下来是 MHA 和 FFN，先看 FFN 模块，它的大概流程如下（@ 表示矩阵/张量乘法）。

z1 = ns @ up_weights
z2 = ns @ gate_weights
z3 = z1 * silu(z2)
z4 = z3 @ down_weights

整体来看是先将网络扩大再收缩，扩大时增加了一个激活处理。silu 函数大概长这样：

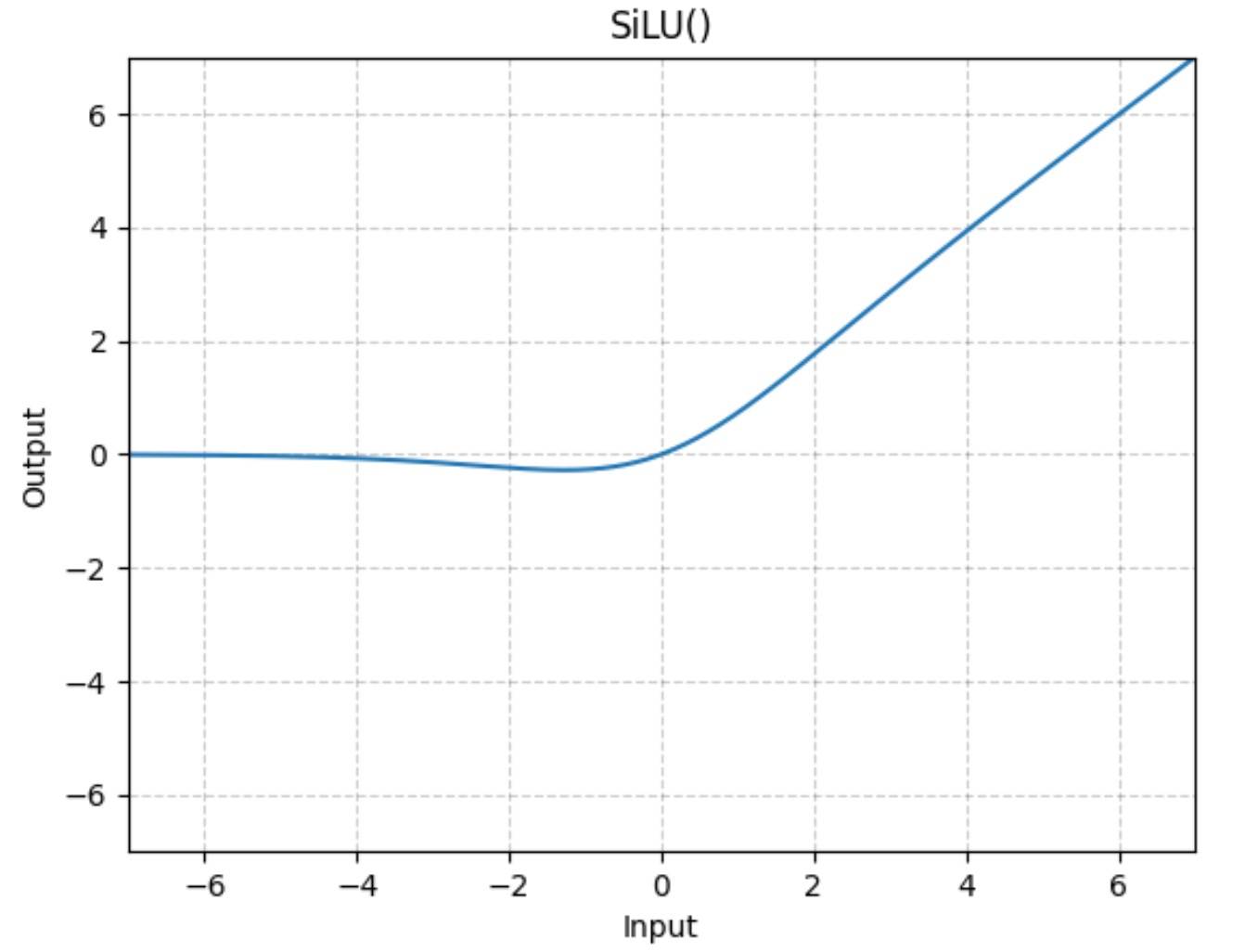
等价于只激活了一部分参数，这个非线性激活非常重要，可以让模型学习到更丰富的知识和表达。

再就是 MHA 模块了，大概流程如下（为了更直观，去掉了 Batch Size 和 Softmax）。

q = ns @ q_weights # (L, D) @ (D, D) = (L, D)
k = ns @ k_weights # (L, D) @ (D, D) = (L, D)
v = ns @ v_weights # (L, D) @ (D, D) = (L, D)

q = q.reshape(L, NH, HD)
k = k.reshape(L, NH, HD)
v = v.reshpae(L, NH, HD)

attn = q.trans(NH, L, HD) @ k.trans(NH, HD, L)  # (NH, L, HD) @ (NH, HD, L) = (NH, L, L)
v = attn @ v.trans(NH, L, HD) # (NH, L, L) @ (NH, L, HD) = (NH, L, HD)
v = v.reshpe(L, NH*HD) # (L, D)

其中，NH 表示 Attention 的 Head 数，HD 表示 Head 的维度。因为有 NH 个 Head，所以叫 Multi-Head，但其实我们看上面的过程，在实际计算的时候它们是合并一起算的。我们不妨只看一个 Head，如下所示。

q = ns @ hq_weights # (L, D) @ (D, HD) = (L, HD)
k = ns @ hk_weights # (L, D) @ (D, HD) = (L, HD)
v = ns @ hv_weights # (L, D) @ (D, HD) = (L, HD)

attn = q @ k.T # (L, HD) @ (HD, L) = (L, L)
v = attn @ v # (L, L) @ (L, HD) = (L, HD)

上面的多个 Head 的 v 就是下面的每个 Head 的 v 拼接起来的。

Multi-Head 是多个注意力头去执行 Attention，其思想是让每个 Head 去捕获不同角度/层面的 Attention，这些角度/层面是什么？不是特别清楚（但一定是某种特征），但我们可以通过 Attention 的权重看出外在 Token 级别的注意力，知道每个注意力 Head，哪些 Token 之间有比较强的连接。

参数

关于 f(x) 我们已经介绍完了，可以发现这个函数其实还是有点复杂的。接下来，我们看看参数情况。

对一个一元一次方程（比如 f(x) = ax + b）来说，参数就两个：a 和 b，但对于 LLM 来说，参数就非常多了，目前常用的是 7B、13B、20B 的级别，也就是 70亿、130亿和 200亿的参数规模。

在神经网络中，可以把矩阵乘法看作是多元一次方程组的计算过程，输入的 Hidden State 维度是 D，就表示未知变量的维度是 D，也就是 D 元一次方程组。

以前面的但 Head Attention 的 q 为例，q_weights 是一个 DxHD 的参数矩阵，我们把 D 和 HD 设置的小一点（假设为4和2），看一个具体的例子。

torch.manual_seed(42)
w = nn.Linear(4, 2, bias=False) # D=4, HD=2
hs = torch.rand((3, 4)) # L=3, D=4
q = hs @ w.weight.T

"""
hq_weights = w.weight.T = 
tensor([[ 0.3823, -0.1096],
        [ 0.4150,  0.1009],
        [-0.1171, -0.2434],
        [ 0.4593,  0.2936]])

hs = 
tensor([[0.9408, 0.1332, 0.9346, 0.5936],
        [0.8694, 0.5677, 0.7411, 0.4294],
        [0.8854, 0.5739, 0.2666, 0.6274]])


q = 
tensor([[ 0.5781, -0.1428],
        [ 0.6784, -0.0923],
        [ 0.8336,  0.0803]])
"""

这个例子除了维度小一点，其他逻辑是一样的。它对应这么一个多元方程组。

w11*x11 + w21*x12 + w31*x13 + w41*x14 = y11
w12*x11 + w22*x12 + w32*x13 + w42*x14 = y12
w11*x21 + w21*x22 + w31*x23 + w41*x24 = y21
w12*x21 + w22*x22 + w32*x23 + w42*x24 = y22
w11*x31 + w21*x32 + w31*x33 + w41*x34 = y31
w12*x31 + w22*x32 + w32*x33 + w42*x34 = y32

其中 x 就是 hs，w 就是 hq_weights，写成数学表达式大概就是下面的这样。 $$ \left[\begin{array}{llll} x_{11} & x_{12} & x_{13} & x_{14} \ x_{21} & x_{22} & x_{23} & x_{24} \ x_{31} & x_{32} & x_{33} & x_{34} \end{array}\right] \times\left[\begin{array}{ll} w_{11} & w_{12} \ w_{21} & w_{22} \ w_{31} & w_{32} \ w_{41} & w_{42} \end{array}\right]=\left[\begin{array}{ll} y_{11} & y_{12} \ y_{21} & y_{22} \ y_{31} & y_{32} \end{array}\right] $$ 对于这样的一个 Linear 来说，参数量就是 2×4=8 个。现在让我们看看 LLaMA，就按词表大小=32000，维度=4096来计算。

首先是 Embedding 和 LM Head（就是映射到 32000 个 Token 的那个参数），它们是一样的，都是 32000×4096，有时候这两个地方的参数也可以设计成共享的，LM Head 前面也有一个 Normalization，4096 个参数。

然后是 Block，MHA 的 qkvo 是 4 个 4096×4096 的矩阵，FFN 的 gate、up、down 是 11008×4096 的矩阵，再加上两个 Normalization， 4096×2 个参数。每个 Block 参数量为 4096×（4096×4+11008×3+2）。

这样得到所有的参数总和为：32000*4096*2 + 4096 +(4096*(4096*4+11008*3+2))*32 = 6738415616，67亿多的样子，也就是常说的 7B。

Rust与LLaMA

终于来到了 Rust，之所以前面铺垫那么多，是因为如果我们完全不熟悉模型的基本结构和执行过程，这个代码看起来就会知其然而不知其所以然。当然，即便了解了基本结构，里面也有一些细节需要单独介绍，不过我们会放在后续的内容。

只看上面的内容，我们可以发现 LLM 模型的结构其实不算特别复杂，而且其中涉及到大量的矩阵运算（至少占到 80% 以上）。关于矩阵运算以及相关的优化，我们也会在后面慢慢涉及。

LLaMA 的 Rust 实现有很多个版本，本次选择的是来自 karpathy/llama2.c: Inference Llama 2 in one file of pure C 的 Rust 实现的版本中的：danielgrittner/llama2-rs: LLaMA2 + Rust，而且我们暂时只会涉及模型基础结构部分，其中涉及一些特别的细节会简单解释，不深入展开。

配置

首先是配置，如下所示。

struct Config {
    dim: usize,        // transformer dimension
    hidden_dim: usize, // for ffn layers
    n_layers: usize,   // number of layers
    n_heads: usize,    // number of query heads
    head_size: usize,  // size of each head (dim / n_heads)
    n_kv_heads: usize, // number of key/value heads
    shared_weights: bool,
    vocab_size: usize, // vocabulary size
    seq_len: usize,    // max. sequence length
}

dim 就是上面一直说的 Dim，hidden_dim 仅在 FFN 层，因为 FFN 层需要先扩大再缩小。n_heads 和 n_kv_heads 是 Query 的 Head 数和 KV 的 Head 数，简单起见可以认为它们是相等的。如果我们加载 karpathy 的 15M 的模型，结果如下。

Config { dim: 288, hidden_dim: 768, n_layers: 6, n_heads: 6, head_size: 48, n_kv_heads: 6, shared_weights: true, vocab_size: 32000, seq_len: 256 }

shared_weights 就是上面提到的 Embedding 和 LM Head 是否共享参数。

Tokenizer 的功能我们暂且略过，目前只需知道它负责将文本转为 ID 列表（encode）以及把 ID 列表转为文本（decode）。

参数

接下来看模型参数，如下所示。

struct TransformerWeights {
    // Token Embedding Table
    token_embedding_table: Vec<f32>, // (vocab_size, dim)
    // Weights for RMSNorm
    rms_att_weight: Vec<f32>, // (layer, dim)
    rms_ffn_weight: Vec<f32>, // (layer, dim)
    // Weights for matmuls in attn
    wq: Vec<f32>, // (layer, dim, dim)
    wk: Vec<f32>, // (layer, dim, dim)
    wv: Vec<f32>, // (layer, dim, dim)
    wo: Vec<f32>, // (layer, dim, dim)
    // Weights for ffn
    w1: Vec<f32>, // (layer, hidden_dim, dim)
    w2: Vec<f32>, // (layer, dim, hidden_dim)
    w3: Vec<f32>, // (layer, hidden_dim, dim)
    // final RMSNorm
    rms_final_weights: Vec<f32>, // (dim)
    // freq_cis for RoPE relatively positional embeddings
    freq_cis_real: Vec<f32>, // (seq_len, head_size/2)
    freq_cis_imag: Vec<f32>, // (seq_len, head_size/2)
    // (optional) classifier weights for the logits, on the last layer
    wcls: Vec<f32>, // (vocab_size, dim)
}

上面的参数应该都比较直观，我们不太熟悉的应该是 freq_ 开头的两个参数，它们是和位置编码有关的参数，也就是说，我们每次生成一个 Token 时，都需要传入当前位置的位置信息。

位置编码在 Transformer 中是比较重要的，因为 Self Attention 本质上是无序的，而语言的先后顺序在有些时候是很重要的，比如 “我喜欢你” 和 “你喜欢我”，“你” 和 “我” 的顺序不同，语义也不同。但时候很多语义又不太响影我们解理语义，不妨再仔细读一下刚刚这半句话。你看文本顺序虽然变了，但你读起来毫无障碍。这也是为什么会有研究说不要位置编码语言模型也可以，但效果应该是不如加了位置编码的。

模型创建好后，接下来就是加载参数和执行推理。加载参数要看模型文件的格式设计，本项目来自 karpathy 的 C 代码，模型文件被安排成了 bin 文件，按规定的格式读取即可，核心代码如下。

fn byte_chunk_to_vec<T>(byte_chunk: &[u8], number_elements: usize) -> Vec<T>
where
    T: Clone,
{
    unsafe {
        // 获取起始位置的原始指针
        let data = byte_chunk.as_ptr() as *const T;
        // 从原始指针创建一个 T 类型的切片，注意number_elements是element的数量，而不是bytes
        // 这句是 unsafe 的
        let slice_data: &[T] = std::slice::from_raw_parts(data, number_elements);
        // 将切片转为 Vec，需要 T 可以 Clone
        slice_data.to_vec()
    }
}

byte_chunk 表示原始的字节切片，number_elements 表示结果向量中元素的个数，T 有 Clone 的 Trait 约束，表示 T 必须实现该 Trait，也就是 T 必须能够使用 Clone 方法。其他解释已经在代码中给出了注释，不再赘述。

加载模型就是读取原始的 bin 文件并指定对应的参数大小，我们以 Token Embedding 参数为例，如下所示。

let token_embedding_table_size = config.vocab_size * config.dim;
// offset.. 表示从 offset 往后的所有元素
let token_embedding_table: Vec<f32> = byte_chunk_to_vec(&mmap[offset..], token_embedding_table_size);

类似这样就可以依次把模型参数读取进来了。

模型

接下来就是最复杂的模型部分了。这里最大的不同是 Token by Token 的处理，而不是给定一个上下文生成下一个 Token。我们看一下基本的 Struct，如下所示。

struct LLaMA2<'a> {
    // buffers for current activations
    x: Vec<f32>,      // activation at current timestep (dim,)
    xb: Vec<f32>,     // same, but inside a residual branch (dim,)
    xb2: Vec<f32>,    // additional buffer (dim,)
    hb: Vec<f32>,     // buffer for hidden dimension in the ffn (hidden_dim,)
    hb2: Vec<f32>,    // buffer for hidden dimension in the ffn (hidden_dim,)
    q: Vec<f32>,      // query (dim,)
    k: Vec<f32>,      // key (dim,)
    v: Vec<f32>,      // value (dim,)
    att: Vec<f32>,    // attention scores (n_heads, seq_len)
    logits: Vec<f32>, // output logits (vocab_size,)
    // kv cache
    key_cache: Vec<f32>,   // (layer, seq_len, dim)
    value_cache: Vec<f32>, // (layer, seq_len, dim)
    // weights & config
    transformer: &'a TransformerWeights,
    config: &'a Config,
}

最后两个参数我们上面已经介绍过了，其他参数都是模型推理过程中需要用到的中间结果和最初的输入，以及最终的结果，它们均被初始化成 0。至于为什么有些值是多个（比如 xb、hb等），是因为 Block 里面涉及到残差连接，需要额外保存一个输入。

现在我们从 forward 开始，方法如下。

fn forward(&mut self, token: usize, pos: usize) {
    // fetch the token embedding
    self.x.copy_from_slice(
        &self.transformer.token_embedding_table
            [(token * self.config.dim)..((token + 1) * self.config.dim)],
    );

    // Note: here it always holds that seqlen == 1 in comparison to the PyTorch implementation
    for l in 0..self.config.n_layers {
        self.layer(l, pos);
    }

    // final RMSNorm
    rmsnorm(
        self.x.as_mut_slice(),
        self.transformer.rms_final_weights.as_slice(),
    );

    // generate logits, i.e., map activations from dim to vocab_size
    matmul(
        self.logits.as_mut_slice(),       // out: (vocab_size,)
        self.transformer.wcls.as_slice(), // W: (vocab_size, dim)
        self.x.as_slice(),                // x: (dim,)
    );
}

这块代码是推理的全流程，一共四个步骤：取 Embedding、逐层计算、Normalization、映射到词表大小的 logits（后续会基于此转为概率分布）。

Embedding 是直接从参数里 copy 出对应索引的参数，无序赘述。

Normalization 用的是 RMS（Root Mean Square）Normalization，基本公式如下。 $$ x'i = \frac{x_i} {\sqrt{\sum{i=1}^N x_i}} * w_i $$ 它是标准 Normalization 的简单形式，但效果尚可，其代码如下。

fn rmsnorm(x: &mut [f32], weight: &[f32]) {
    let size = x.len();

    let squared_sum = x.iter().fold(0.0, |acc, x| acc + x * x);
    let rms = 1. / (squared_sum / size as f32).sqrt();

    x.iter_mut()
        .zip(weight.iter())
        .for_each(|(x, w)| *x *= rms * w);
}

代码一目了然，先一个 reduce，然后开方取倒数，接着就是遍历计算更新每个参数值。

最后的矩阵乘法比较标准，输入的 Hidden State（x）因为只有一个 Token，所以可以看成向量，长度为 Dim，与 LM Head 矩阵乘法后就得到一个词表大小的输出值，后续可以归一化成概率值（即概率分布）。矩阵乘法代码如下（准确来说是向量和矩阵乘法）。

fn matmul(target: &mut [f32], w: &[f32], x: &[f32]) {
    let in_dim = x.len();
    target.par_iter_mut().enumerate().for_each(|(i, t)| {
        let row_offset = i * in_dim;
        *t = x
            .iter()
            .zip(w[row_offset..].iter())
            .fold(0.0, |result, (x, w)| result + x * w);
    });
}

这里需要注意的是 offset，因为参数是一个 Vec 存储的一维数组，要按二维取值，需要每次跳过对应数量的参数。剩下的就很清晰了，最终的结果会存储到 target，也就是 self.logits，进而会转为概率分布。

我们把重心放在中间的逐层计算上，LLM 的核心也在这里。先看 layer 的代码，如下所示。

fn layer(&mut self, layer: usize, pos: usize) {
    // Note: we leave the buffer x as it is because we need it for the residual connection
    rmsnorm_with_dest(
        self.xb.as_mut_slice(),
        self.x.as_slice(),
        &self.transformer.rms_att_weight
            [layer * self.config.dim..(layer + 1) * self.config.dim],
    );
    self.attn(layer, pos);
    // residual connection
    add_vectors(self.x.as_mut_slice(), self.xb2.as_slice());

    // Note: we leave the buffer x as it is because we need it for the residual connection
    rmsnorm_with_dest(
        self.xb.as_mut_slice(),
        self.x.as_slice(),
        &self.transformer.rms_ffn_weight
            [layer * self.config.dim..(layer + 1) * self.config.dim],
    );
    self.ffn(layer);
    // residual connection
    add_vectors(self.x.as_mut_slice(), self.xb.as_slice());
}

非常标准的流程（可回看前面的架构图），先归一化，然后 MHA，残差连接，再归一化，FFN，残差连接。归一化的代码刚刚已经看过了，这里唯一的不同是将输出放到第一个参数（即 self.xb）里。add_vectors 就是对应元素值求和，结果放到第一个参数，这个比较简单，我们就不放代码了。重点就是 ffn 和 attn，它们内部涉及大量矩阵乘法，我们开始。

先看 ffn，它比较简单，主要是几个矩阵乘法加非线性激活，代码如下。

fn ffn(&mut self, layer: usize) {
    let weight_from = layer * self.config.hidden_dim * self.config.dim;
    let weight_to = (layer + 1) * self.config.hidden_dim * self.config.dim;

    // gate z2
    matmul(
        self.hb.as_mut_slice(),                       // out: (hidden_dim,)
        &self.transformer.w1[weight_from..weight_to], // W: (hidden_dim, dim)
        self.xb.as_slice(),                           // x: (dim,)
    );

    // up z1
    matmul(
        self.hb2.as_mut_slice(),                      // out: (hidden_dim,)
        &self.transformer.w3[weight_from..weight_to], // W: (hidden_dim, dim)
        self.xb.as_slice(),                           // x: (dim,)
    );

    // z3
    for i in 0..self.config.hidden_dim {
        self.hb[i] = silu(self.hb[i]) * self.hb2[i];
    }

    // down z4
    matmul(
        self.xb.as_mut_slice(),                       // out: (hidden_dim,)
        &self.transformer.w2[weight_from..weight_to], // W: (hidden_dim, dim)
        self.hb.as_slice(),                           // x: (dim,)
    );
}

这个过程和我们《开源代表——LLaMA 结构》一节中是一一对应的，涉及到的主要是刚刚介绍过的 matmul 和一个 silu，后者我们之前看过它的图像，代码如下。

fn silu(x: f32) -> f32 {
    x / (1.0 + (-x).exp())
}

表达式如下所示。 $$ \text{SiLU}(x) = \frac{x}{1 + e^{-x}} $$ 好了，最后我们把重心放在 attn 这个方法上，由于逐 Token 生成时，Query 是当前 Token，这没问题，但 Key 和 Value（Attention 里面的 K和V）是需要历史 Token 的（不然怎么算注意力）。常见的做法就是把历史过程中的 K 和 V 缓存起来，每次生成时顺便更新缓存，这样下次生成时拿到的就是之前的所有 K 和 V。

先看一下基本的代码流程，如下所示。

fn attn(&mut self, layer: usize, pos: usize) {
    // qkv matmuls
    self.attn_qkv_matmuls(layer);

    // apply RoPE rotation to the q and k vectors for each head
    self.attn_rope(layer, pos);

    // Multi-head attention with caching
    self.cache_kv(layer, pos);
    self.multihead_attn(layer, pos);

    // wo
    let weight_from = layer * self.config.dim * self.config.dim;
    let weight_to = (layer + 1) * self.config.dim * self.config.dim;
    matmul(
        self.xb2.as_mut_slice(),                      // out: (dim,)
        &self.transformer.wo[weight_from..weight_to], // W: (dim, dim)
        self.xb.as_slice(),                           // x: (dim,)
    );
}

最后的 wo 比较简单，不再赘述。一开始的 qkv 也比较简单，都是矩阵乘法，如下所示。

fn attn_qkv_matmuls(&mut self, layer: usize) {
    let weight_from = layer * self.config.dim * self.config.dim;
    let weight_to = (layer + 1) * self.config.dim * self.config.dim;

    matmul(
        self.q.as_mut_slice(),                        // out: (dim,)
        &self.transformer.wq[weight_from..weight_to], // W: (dim, dim)
        self.xb.as_slice(),                           // x: (dim,)
    );

    matmul(
        self.k.as_mut_slice(),                        // out: (dim,)
        &self.transformer.wk[weight_from..weight_to], // W: (dim, dim)
        self.xb.as_slice(),                           // x: (dim,)
    );

    matmul(
        self.v.as_mut_slice(),                        // out: (dim,)
        &self.transformer.wv[weight_from..weight_to], // W: (dim, dim)
        self.xb.as_slice(),                           // x: (dim,)
    );
}

还剩下三个方法：attn_rope、cache_kv 和 multihead_attn，我们分别看一下。

第一个用来加入位置信息，参数是一开始算好的，这里直接取出对应位置的值进行计算。代码如下所示。

fn attn_rope(&mut self, layer: usize, pos: usize) {
    // apply RoPE rotation to the q and k vectors for each head

    let freq_cis_real_offset = pos * self.config.head_size / 2;
    let freq_cis_imag_offset = pos * self.config.head_size / 2;

    for i in (0..self.config.dim).step_by(2) {
        let q0 = self.q[i];
        let q1 = self.q[i + 1];

        let k0 = self.k[i];
        let k1 = self.k[i + 1];

        let cos = self.transformer.freq_cis_real
            [freq_cis_real_offset + (i % self.config.head_size) / 2];
        let sin = self.transformer.freq_cis_imag
            [freq_cis_imag_offset + (i % self.config.head_size) / 2];

        self.q[i] = q0 * cos - q1 * sin;
        self.q[i + 1] = q1 * cos + q0 * sin;

        self.k[i] = k0 * cos - k1 * sin;
        self.k[i + 1] = k1 * cos + k0 * sin;
    }
}

这部分代码就是把位置信息注入到 Q 和 K 中，其理论分析比较复杂，此处不展开。

cache_kv 比较简单，直接把当前的 K 和 V 存起来即可，如下所示。

fn cache_kv(&mut self, layer: usize, pos: usize) {
    // cache the key, value for the current timestep (pos)
    let layer_offset = layer * self.config.seq_len * self.config.dim; // offset to get to the cache of the current layer
    let cache_from = layer_offset + pos * self.config.dim;
    let cache_to = layer_offset + (pos + 1) * self.config.dim;

    self.key_cache[cache_from..cache_to].copy_from_slice(&self.k.as_slice());
    self.value_cache[cache_from..cache_to].copy_from_slice(&self.v.as_slice());
}

因为我们不确定用户生成的 Token 长度，所以就把最大长度（seq_len）的所有位置都占上，因为是按层存的，每一层都有计算，所以需要层的 ID。每一层、每个位置都缓存 dim 个中间结果。

最后就是最重要的 multihead_attn 了，这里面的主要逻辑是计算 attention 分数，然后得到 attention 之后的结果，代码如下。

fn multihead_attn(&mut self, layer: usize, pos: usize) {
    // offset to get to the cache of the current layer
    let layer_offset_for_cache = layer * self.config.seq_len * self.config.dim; 
    // 缩放因子
    let sqrt_d = (self.config.head_size as f32).sqrt();
	
    // att 和 xb 分别按指定大小切块
    // attn_scores每一块是seq_len长度，共n_head(NH)块，即按 head 处理
    // xb每一块是head_size长度，共n_head(NH)块
    self.att.par_chunks_exact_mut(self.config.seq_len)
        .zip(self.xb.par_chunks_exact_mut(self.config.head_size))
        .enumerate()
        .for_each(|(h, (attn_scores, xb))| {
            assert_eq!(attn_scores.len(), self.config.seq_len);
            assert_eq!(xb.len(), self.config.head_size);

            // get query vector of the timestep pos for the current head
            // 第h个head，Q是当前Token，(1, HD)
            let q_from = h * self.config.head_size;
            let q_to = (h + 1) * self.config.head_size;
            let q = &self.q[q_from..q_to];

            // Compute temp = (K * q_pos) / sqrt(dim)
            // K和V是要包含历史Token，(L, HD)
            // q @ k.T 得到的是 (1,HD)@(HD,L)=(1, L) 大小的 attention score
            // 这里循环L（pos）次，所以每一个位置的值是 (1,HD)@(HD,1)=(1,1)，即点积
            for t in 0..=pos {
                // key_cache[l, t]
                let timestep_and_layer_offset = layer_offset_for_cache + t * self.config.dim; 
                // for the current key, select the correct range which corresponds to the current head
                let key_vector_from = timestep_and_layer_offset + h * self.config.head_size;
                let key_vector_to = timestep_and_layer_offset + (h + 1) * self.config.head_size;
                let key_vector = &self.key_cache[key_vector_from..key_vector_to];

                attn_scores[t] = inner_product(q, key_vector) / sqrt_d;
            }

            // softmax the scores to get attention weights, from 0..pos inclusively
            // 归一化得到概率
            softmax(&mut attn_scores[..(pos + 1)]);

            // Compute temp2^T * V
            // 计算加权的v
            // attention是 (1,L)，V是(L,HD)，每个HD的权重是attention[i]
            xb.fill(0.0);

            for t in 0..=pos {
                // value_cache[l, t]
                let timestep_and_layer_offset = layer_offset_for_cache + t * self.config.dim; 
                // for the current value, select the correct range which corresponds to the current head
                let value_vector_from = timestep_and_layer_offset + h * self.config.head_size;
                let value_vector_to = timestep_and_layer_offset + (h + 1) * self.config.head_size;
                let value_vector = &self.value_cache[value_vector_from..value_vector_to];
                
                // weighted sum with attention scores as weights
                let attention_weight = attn_scores[t];
                for i in 0..self.config.head_size {
                    xb[i] += attention_weight * value_vector[i];
                }
            }
        });
}

上面的过程是分 Head 计算的，需要我们深刻理解前面《开源代表——LLaMA 结构》一小节的内容，具体解释可以参考代码里的注释。值得一提的是，分 Head 计算是并行的。

另外，有个新方法 inner_product 是点积，也就是对应元素相乘后求和，代码如下。

fn inner_product(x: &[f32], y: &[f32]) -> f32 {
    zip(x, y).fold(0.0, |acc, (a, b)| acc + a * b)
}

比较简单，不再赘述。

生成

最后就是生成（或 Decoding）过程。代码略有不同，我们先看下。

fn generate(&mut self, prompt_tokens: &Vec<usize>, n_tokens: usize, temperature: f32) -> Vec<usize> {
    let mut tokens = vec![];
    tokens.reserve(n_tokens);

    let mut token = BOS_TOKEN;
    tokens.push(token);

    // forward through the prompt to fill up the KV-cache!
    for (pos, prompt_token) in prompt_tokens.iter().enumerate() {
        self.forward(token, pos);
        token = *prompt_token;
        tokens.push(token);
    }

    // complete the prompt
    for pos in prompt_tokens.len()..(n_tokens - 1) {
        self.forward(token, pos);

        if temperature == 0.0 {
            token = argmax(self.logits.as_slice());
        } else {
            // Apply temperature and then sample.
            self.logits.iter_mut().for_each(|p| *p = *p / temperature);
            softmax(&mut self.logits.as_mut_slice());
            token = sample(self.logits.as_slice());
        }

        tokens.push(token);
    }

    tokens
}

这里有两个值得注意的地方。

第一个是推理 Prompt（即第一次输入时的 Context），此时给定的 Context 是多个 Token 组成的，执行该过程目的是填充 KV Cache。

第二个是采样过程，temperature=0.0 时，就是 Greedy Search，每次返回概率最大位置的 Token；否则，会先应用 temperature，然后按照概率分布进行采样。temperature 参数会平滑概率分布，值越大，平滑力度越大，更有可能生成多样的结果。softmax 用来把一系列值归一化成概率分布（所有值加起来和为 1.0）。我们重点看看这个 sample 方法，它的主要思想是根据概率分布进行采样，也就是高概率的位置更容易被采样到，低概率的位置更不容易被采样到。代码如下。

fn sample(probs: &[f32]) -> usize {
    let mut rng = rand::thread_rng();
    let mut cdf = 0.0;
    let r = rng.gen_range(0.0..1.0);
    for (i, p) in probs.iter().enumerate() {
        cdf += p;
        if cdf > r {
            return i;
        }
    }
    probs.len() - 1
}

随机生成 0-1 之间的一个值（均匀分布），计算累积概率，当累积概率大于刚刚生成的值时，返回此时的位置。这样就可以保证是按照概率分布进行采样的。我们举个具体的例子，如下所示。

// 假设概率分布为
probs = [0.1, 0.2, 0.1, 0.5, 0.1]
// 累积概率为
accu_probs = [0.1, 0.3, 0.4, 0.9, 1.0]

假设随机值为 r，因为它是均匀分布的，所以落在不同区间的概率与该区间的长度成正比。我们看上面的累积概率，可以得出如下结果。

r落在区间	返回 Index
[0, 0.1)	0
[0.1, 0.3)	1
[0.3, 0.4)	2
[0.4, 0.9)	3
[0.9, 1.0)	4

也就是说返回 Index=3 的概率为 0.5，其他同理。

拿到 Token 向量后只要用 Tokenizer 解码即可得到生成的文本。

小结

本文我们首先简单介绍了 LLM 相关的背景，着重讨论了关于 Token 和生成过程，这是应用 LLM 时非常重要的两个知识点。然后我们介绍了开源 LLM 的代表——LLaMA 的模型结构和参数，给大家一个整体的感知和认识。最后就是 Rust 的实现，主要包括配置、参数、模型和生成四个方面，其中最重要的就是模型部分，模型部分最重要、也最难理解的是 Multi-Head Attention 的计算。主要是因为具体的计算过程都是把矩阵运算给展开了，这需要对模型有一定程度的理解。

这种展开的写法其实是比较底层的实现，如果能在上面抽象一层，直接操纵矩阵或张量，那计算起来应该会简单很多。事实上，大部分框架都是这么做的，比如 Python 的 NumPy 、PyTorch等，当然 Rust 也有类似的框架，比如 NumPy 对应的 ndarray，以及 Rust 版本的深度学习框架。使用这些框架时，我们使用的是矩阵/张量（或者叫多维数组）这个对象，所有的操作也都在这个粒度进行，这无疑极大地提高了编程效率。同时，还可以利用这些框架底层的性能优化。

不过，有时候当我们需要框架暂未支持的更细致的优化、或在一个框架不支持的设备上运行时，这种 Pure X（此处为 Rust）的方式就比较方便灵活了。

总的来说，算法是多样的，实现更是多样的，优化更更是无止境的，吾辈唯有不断前行，持续向上。